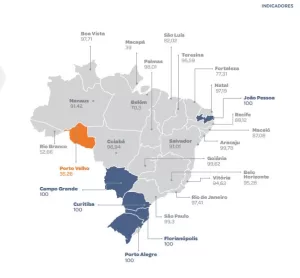
O Instituto Brasileiro de Geografia e Estatística (IBGE) divulgou dados do Produto Interno Bruto (PIB) de 2020...
Conter discursos de ódio e antidemocráticos. Essas são algumas das razões que levaram o ministro do STF...
A Universidade Estadual do Maranhão (Uema) promove, entre os dias 24 de abril e 20 de...
Neste sábado (20), o Conjunto Roseana Sarney recebeu a quinta edição do “Paço em Ação”, evento promovido...
Os 275 novos alunos do Colégio Militar Tiradentes I receberam a boina vermelha, símbolo das escolas militares,...
A Rádio Mirante AM anunciou, na última terça-feira (16), a sua nova cara face à migração para...
Mais de 20 instituições federais de ensino estão em greve e outras sete devem aderir, a partir da próxima semana....